Or, Big Numbers in Python
Background
While browsing YouTube, I happen to come across something called the Wallis Product. No, it is not named after the CEO of Dunder Mifflin, but rather the English mathematician John Wallis. Essentially, it is an infinite product that converges to \(\pi/2\), defined as
\[\begin{align*} \frac{\pi}{2} &= \prod_{n=1}^{\infty}\frac{4n^2}{4n^2-1} = \prod_{n=1}^{\infty}\bigg(\frac{2n}{2n-1}\cdot\frac{2n}{2n+1}\bigg) \\ &= \bigg(\frac{2}{1}\cdot\frac{2}{3}\bigg)\cdot \bigg(\frac{4}{3}\cdot\frac{4}{5}\bigg)\cdot \bigg(\frac{6}{5}\cdot\frac{6}{7}\bigg)\cdot \cdots \end{align*}\]By no means do I intend to prove this here (there are plenty of proofs all around the internet). Instead, I thought it would be fun to visualize this product using Python.
Analysis
What I thought would be a quick one-and-done visualization, actually led to something (slightly) more interesting. I first went about this by pre-populating two lists, one would be the numerator product \(u_n=2,2,4,4,\cdots\) and one would be the denominator product \(d_n=1,2,2,5,\cdots\). For some reason, I then had the bright idea to first calculate the entire numerator product, then the entire denominator product, and then divide those two gargantuan numbers. When plotting the product, I unsurprisingly ended up with the following:
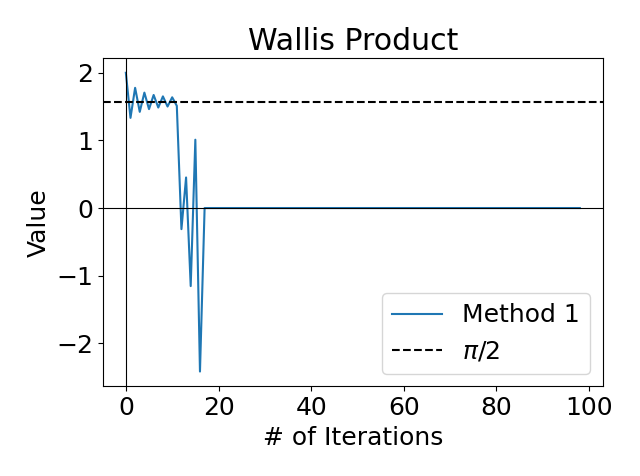
There is some convergence at the beginning, but after about \(n=12\) there is no more convergence to \(\pi/2\), and then around \(n=\) in fact it seems like it goes to zero. But really, the floating-point arithmetic utilized by Python started bugging out. Around \(n=12\), the numerator is equal to
\[2\cdot 2\cdot 4\cdot 4\cdot 6\cdot 6\cdot 8\cdot 8\cdot 10\cdot 10\cdot 12\cdot 12\cdot = 2,123,366,400\]which is also about 1% of Jeff Bezos’ net worth in US dollars. Note that in this method, I iterate through each individual fraction, instead of how the terms were defined in the equation above. So the numerator product is \(u_n=2\cdot 2\cdot 4\cdots\) and the denominator product \(d_n=1\cdot 3\cdot 3\cdots\). So, it was clear to see why my code was bugging out - as these numbers got factorially larger, the computer could not process them. There’s probably a more elegant explanation here, but these are my quick observations.
I decided to then calculate this product using two other methods. For the second method, I made the simple fix of swapping the order of operations: using my pre-populated list, instead of numerator product divided by denominator product, I took the product of each individual fraction one at a time. For the third method, I simply used the formula above instead of using the pre-populated lists in my code. I thought they would be the same, but actually, they were different:
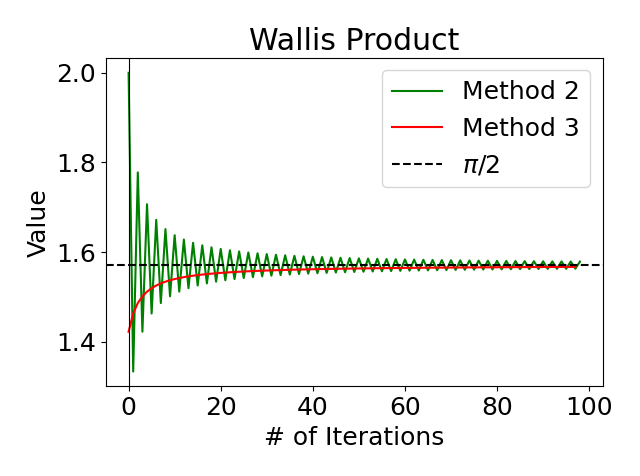
There’s really no magic going on here, as this difference is due to the fact that when I use my pre-populated list (Method 2), the iteration is through each individual fraction, giving it that oscillating convergence. So the terms are
\[\begin{align*} n_1 &= \frac{2}{1} = 2 \\ n_2 &= \frac{2}{1}\cdot\frac{2}{3} \approx 1.33 \\ n_3 &= \frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3} \approx 1.77 \end{align*}\]and so on. When using the formula (Method 3), convergence was achieved without any oscillation, because these terms are essentially the same terms in Method 2, just multiplied in pairs. So the terms for Method 3 are
\[\begin{align*} n_1 &= \bigg(\frac{2}{1}\cdot\frac{2}{3}\bigg) \approx 1.33 \\ n_2 &= \bigg(\frac{2}{1}\cdot\frac{2}{3}\bigg) \cdot \bigg(\frac{4}{3}\cdot\frac{4}{5}\bigg) \approx 1.42 \\ n_3 &= \bigg(\frac{2}{1}\cdot\frac{2}{3}\bigg) \cdot \bigg(\frac{4}{3}\cdot\frac{4}{5}\bigg) \cdot \bigg(\frac{6}{5}\cdot\frac{6}{7}\bigg) \approx 1.46 \end{align*}\]Since the value of \(\pi/2 \approx 1.57079632679\), it is clear to see that Method 2 oscillates above and below this value, while Method 3 starts below this value and slowly creeps up to it.
There’s really not much else I did here, but it was interesting to me and I figured I’d share. The python code I used can be downloaded here, for those interested.
